فضاهای متریک فازی حاصلضربی
فضاهای متریک فازی حاصلضربی
انجام پایان نامه ریاضی
فضاهای متریک فازی حاصلضربی و برخی از ویژگی های توپولوژیکی
ما مفهوم فضای متریک فازی در تعریف جورج و ویرامانی را با ارائه تعریف فضای متریک فازی حاصلضربی و ایجاد فضای متریک پیوند یافته فازی، ایجاد می کنیم.
ما همچنین برخی از نتایج شناخته شده فضاهای متریک از جمله قضیه بایر برای فضاهای متریک فازی ضربی با قطر نقص را اثبات می کنیم.
مقدمه
در سال 1965 ، نظریه مجموعه های فازی توسط زاده ابداع شد [16].
پس از آن متون بسیاری در زمینه منطق فازی و مجموعه های فازی مانند [4 ، 14] منتشر شده است.
جورج و ویرامانی با ایجاد اصلاحاتی، فضای متریک فازی را دوباره تعریف کردند، که توسط کراموسیل و میچاک در [10] معرفی شد و نتایج جدیدی را در فضاهای متریک فازی ارائه داد [5 ، 6].
از سویی دیگر در سال 1972 گروسمن و كاتز محاسبات جدیدی به نام محاسبات غیر نیوتونی را در ادامه محاسبات کلاسیک ایجاد كردند [8].
آنها برای ایجاد این محاسبات، از مولدهای افزایشی استفاده کردند. به عنوان یک مورد خاص از مولدها ، تابع نماییe محاسبات ضربی (یا هندسی) ایجاد می کند.
بشیروف و همکاران. بر روی محاسبات ضربی مطالعه و برخی از خواص کلاسیک مشتقات و انتگرال در حوزه محاسبات ضربی [2].
را ترمیم کرد. س.کامک و باسار اعداد طبیعی حقیقی از اعداد حقیقی غیر نیوتونی و مفهوم متریک غیر نیوتونی را ساختند [5].
بینباس و همکاران[3] و کریس [9] برخی از خصوصیات توپولوژیکی مربوط به فضاهای متریک غیر نیوتونی را تعریف کردند.
اگر فکر می کنید هیچ مولدی نمی تواندافزایشی باشد، ما تعریف متریک غیر نیوتونی را مجددا تفسیر می کنیم و آن را متریک مولد می نامیم.
سپس ما مفهوم فضای متریک فازی را با ارائه مفاهیم متریک فازی ضربی و متریک پیوندی فازی ضربی تعریف می کنیم.
در این حالت ، هنگامی که مولد را به عنوان تابع شناسایی در نظر می گیریم بدیهی است که هر متریک فازی یک متریک فازی حاصل ضربی است.
در پایان ، ما چند قضیه راجع به همگرایی دنباله ها و قضیه بایر را بررسی می کنیم که در آنالیز تابعی و فضاهای توپولوژیکی [1 ، 13] برای فضاهای متریک فازی ضربی قرار دارد را با کمک مفهوم قطر ناقص α- متفاوت از [6] و [7] اثبات می کنیم.
نگارش مقاله ریاضی
پیش نیاز
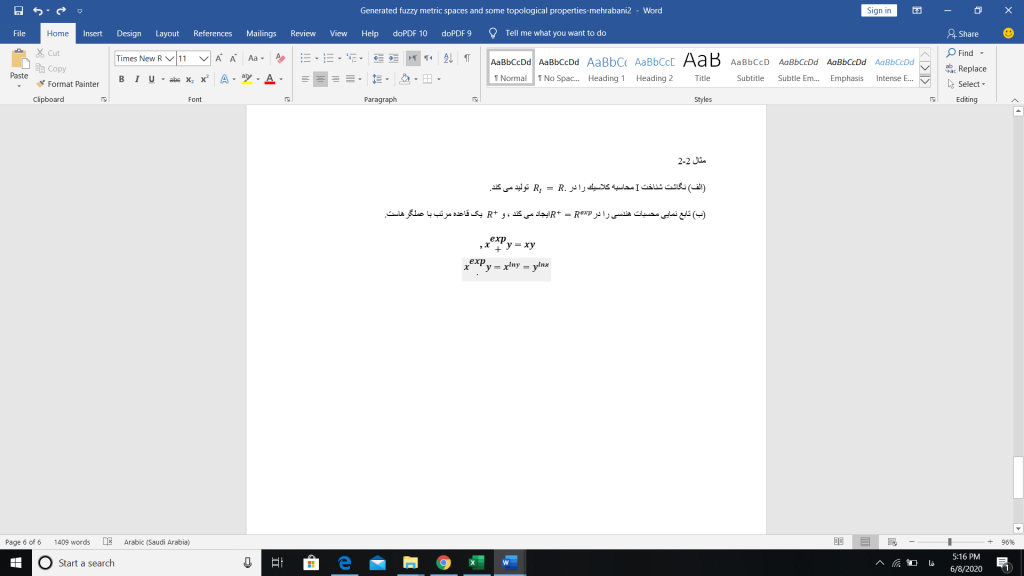
حاصل α یک نگاشت یک به یک است که دامنه آن R است و برد آن Rα (یا R (N)) زیر مجموعه ای از R است. هر مولد دقیقاً یک محاسبه و برعکس هر محاسبه دقیقا توسط یک مولد تولید می شود. چهار عمل دودویی اصلی بر روی Rα حاصل α وجود دارد.
بعلاوه عملیات جمع و ضرب α در Rα توسط تعریف شده است.



Abstract.
We generalize the concept of fuzzy metric space in the sense of George and Veeramani by presenting the definition of generated fuzzy metric space and generated fuzzy bonded metric space.
We prove also some known results of metric spaces including Baire’s theorem for generated fuzzy metric spaces through α-defective diameter.
Introduction
In 1965, the theory of fuzzy sets was discovered by Zadeh [16]. Later, many writings on the fuzzy logic and fuzzy sets have been published as in [4, 14].
Making some modifications George and Veeramani redefined the fuzzy metric space, which was introduced by Kramosil and Michalek in [10], and gived some new results on the fuzzy metric spaces [5, 6].
On the other hand in 1972 Grossman and Katz established a new calculus, called non-Newtonian calculus, alternatively to the classical calculus [8].
Creating this calculus, they used increasing generators. As a special case of generators the exponential function exp generated multiplicative (or geometric) calculus. Bashirov et al.
studied on the multiplicative calculus and restated some classical properties of derivatives and integrals in the realm of multiplicative calculus [2].
C¸ akmak and Bas¸ar constructed the field R(N) of non-Newtonian real numbers and the concept of non-Newtonian metric [5]. Binbas¸ıo˘glu et.al [3] and Kiris¸ci [9] defined some topological properties related to non-Newtonian metric spaces.
Thinking any generator may not be increasing, we reinterpret the definition of non-Newtonian metric and call generated metric.
After that, we generalize the concept of fuzzy metric space by presenting the definition of generated fuzzy metric and generated fuzzy bonded metric.
In this case, it is obviously that every fuzzy metric is a generated fuzzy metric when we take the generator as the identity function .
Finally, we examine some theorems about convergence of sequences and Baire’s theorem which are located in functional analysis and topological spaces [1, 13] for generated fuzzy metric spaces, and prove with help of the concept of α-defective diameter as different from [6] and [7].
برای مشاده مطالب بیشتر به سایت www.farzdon.ir مراجعه نماید.